本页面包含AMC8高频考点、AMC8考试大纲、AMC8知识点和学校知识点比较、AMC8各年级题目考察内容、AMC8答题技巧和注意事项、AMC8竞赛难度分析。
一、AMC8高频考点
AMC8竞赛考点涵盖了小学全部的数学知识和部分的初中知识,旨在全面考察学生的数学知识和思维能力。
1. 基础代数
基础代数是AMC8考试中出现频率最高的考点之一,通常约占10道题目。代数的核心内容涵盖了以下知识点:
分数:学生需要熟练掌握分数的加减乘除运算,以及如何进行分数的简化和比较。
方程:包括简单的一元一次方程的解法,学生需能够独立设置和求解方程。
数列:理解数列的基本概念,能够识别和生成简单的数列,如等差数列和等比数列。
代数不仅是AMC8的核心部分,也是后续更高级别数学学习的基础
2. 基础几何
基础几何的题目数量虽然低于代数,通常约为6-8道,但其考察内容依然非常重要。主要涉及的知识点包括:
三角形:理解三角形的性质,包括角的关系、边的长度等。
四边形:掌握不同类型四边形的特性,如矩形、正方形和菱形等。
勾股定理:能够应用勾股定理解决与直角三角形相关的问题。
主要注意的是:大部分几何内容在国际课程中可能没有涉及,学生应通过额外的学习和练习来补充相关知识。
3. 基础数论
基础数论在AMC8的考察比例逐渐增加,通常占3-4道题目。主要考察的内容包括:
整除:理解整除的概念,能够判断一个数是否可以被另一个数整除。
质因数分解:掌握质因数分解的基本方法,能够将合数分解为质数的乘积。
数论题目通常涉及较为基础的概念,但对于学生的逻辑思维能力有较高的要求。
4. 基础组合
组合题目在AMC8中相对较少,通常约为3-5道,主要涉及计数和概率等内容。重点考察以下知识点:
计数:通过排列和组合的方法解决问题,理解基本的计数原理。
概率:能够计算简单事件发生的概率,理解概率的基本概念。
其中,计数题是每年必考的内容,学生应特别重视这一部分的复习。
(返回顶部)
二、AMC8考试大纲
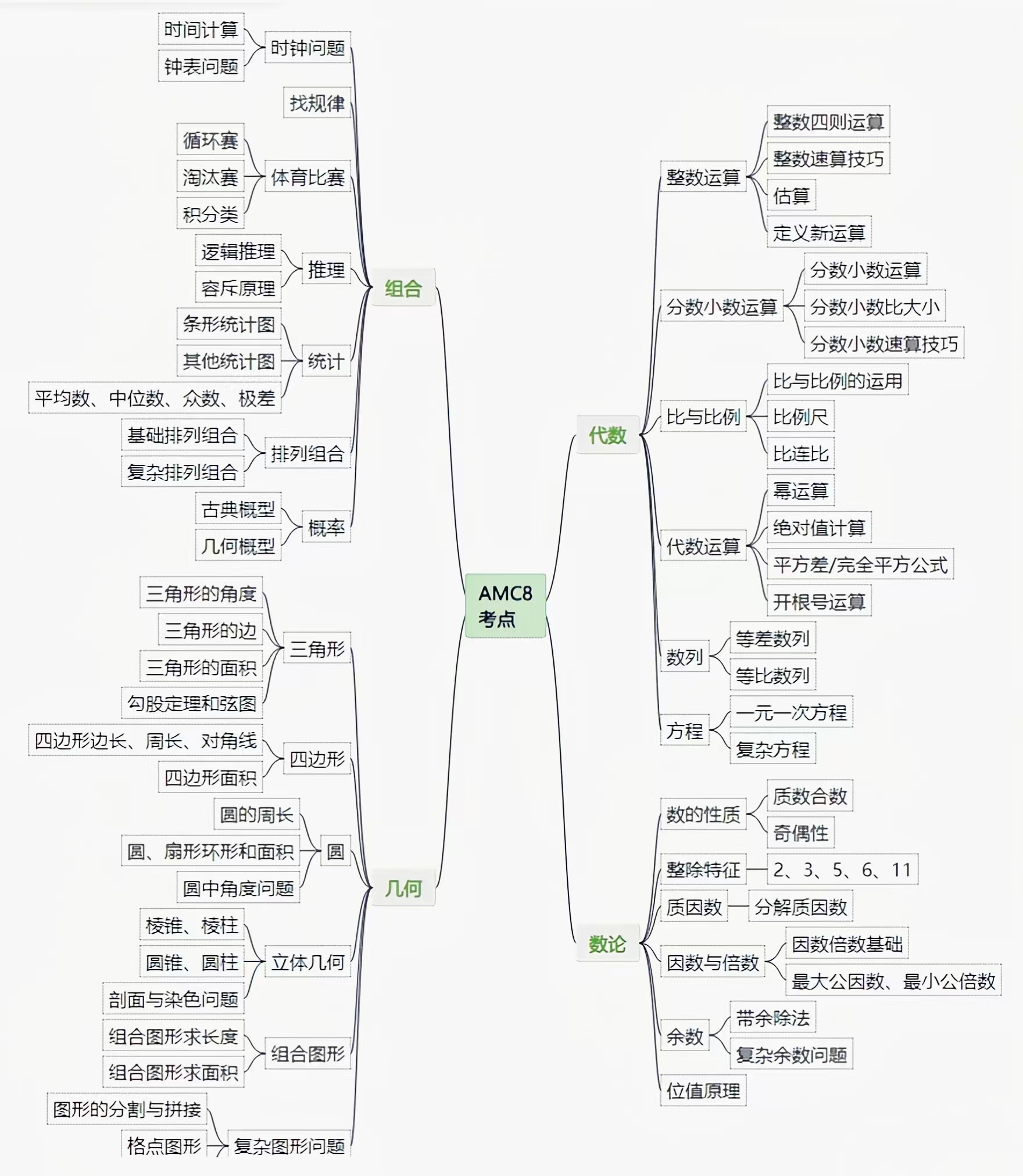
(返回顶部)
三、AMC8知识点和学校知识点比较
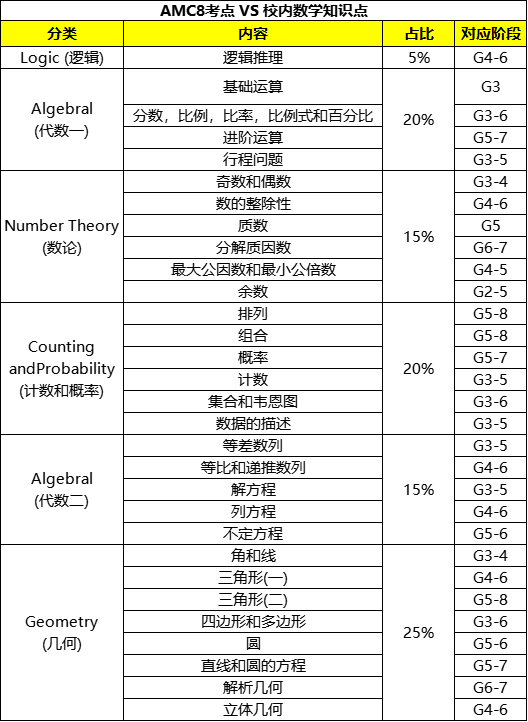
(返回顶部)
四、AMC8题目方向
考察内容:从历年AMC8竞赛题目分析得出,题目主要分为三个方向:小学数学、初中数学和小学奥数。其中有部分图表问题夹在小学数学、小奥和初中数学之间,划定范围模棱两可,但基于专业学科老师分析,基本上可以认为上述三类题目范畴各占1/3。
小学阶段考察范畴
①基本的计算与应用题:整数分数小数以及混合的四则运算,百分比以及比与比例运算类型应用题,行程和相关变形的问题,平均数、中位数、众数等统计问题等;
②基础几何:简单的三角形、四边形与圆形等求角、求边求面积的计算,常见且基础的立体图形或需要空间想象的图形有关计算问题;
③简单数论:质数与合数,约数和倍数以及最大公约数、最小公倍数和整除性质应用有关问题;
小学奥数考察范畴
①巧算和应用题:整数分数小数以及混合运算的巧算,计算找规律,多种不同类型的更深入的应用题,例如鸡兔同笼、青蛙跳井问题、植树问题、工程问题、行船流水与环形跑道问题等:
② 几何求值:利用割补方法求复杂图形面积;
③数论延伸:质因数分析问题、约数个数计算、奇数偶数特点与奇偶性分析问题、余数问题、位置原理有关的问题,以及填数阵图、解竖式类型的计算与数论综合应用题;
计数与组合杂题:阶乘运算,图形计数、找规律计数、加法与乘法原理,举法与分类讨论,容斥原理等,逻辑推理问题,游戏与操作对策问题;
初中阶段考察范畴
①代数:乘方运算、多项式、一次与二次方程、列方程或方程组解应用题、不等式等差数列和等比数列及其有关计算、一次函数及其计算,文字与图表相结合的常见应用题,复杂的利用代数方法解决的统计学问题;
②几何:坐标系有关问题,平面几何中的三角形、四边形、圆形与扇形的定理与性质图形的全等与相似及其在计算中的应用、勾股定理与计算,圆柱和圆锥等立体几何图形;
(返回顶部)
五、AMC8答题技巧和注意事项
1、额外的答题技巧
在AMC8竞赛中,除了常规的解题方法外,巧妙的解题技巧和合理的猜测(smart guess)也能帮助我们提高答题效率和准确率。以下是一些常见的技巧:
代值法、特殊值法和选项结合法:在涉及比与比例、百分比的问题中,当总数未知且总数不影响答案时,可以假设一个总数来进行计算。在数论的整数性分析问题中,可以使用特殊值法结合选项排除法来找到正确答案。例如,可以假设某个变量为一个方便计算的数,从而简化问题。
作图与几何问题:AMC8的几何题通常附有标准配图。在时间紧张或思路不清晰时,可以尝试直接测量图中的参数来快速推理出答案。这种方法尤其适用于那些视觉化的几何问题。
排除法:根据奇偶性、平方数、质数性等特征,可以排除不符合要求的选项。例如,如果题目要求找一个质数,而某个选项明显不是质数,则可以直接排除。
找规律:从最简单的初始情况开始研究,找到大致规律后,再延伸验证。这种方法在处理递归关系或数列问题时尤为有效。
2、要规避的错误
避免计算错误:在计算过程中,尽量少跳步,多打草稿,并进行复算检查。时间紧张时,可以采用个位数检查的方法快速验证计算结果。
避免理解题意错误:注意题目中的关键词和关键条件,例如“包括、排除”,“奇数、偶数”,“质数、合数”,“整数、实数、正数、非负数”等。特别要注意提问部分,准确理解题目所问的问题。对关键条件和关键词划线标注,以避免遗漏。
避免方法选择错误:审题后,不要急于演算和作答。先判断题目类型,思考题目是否存在多解或巧解,然后选择最适当的方法求解,以避免因方法选择错误而浪费时间。
3、考试注意事项
时间安排和答题策略:根据自己的学习和备考水平,提前确定实际考试中的时间安排和答题策略。合理分配时间,确保有足够的时间处理难题。
充分准备常考题型:对于AMC8常考的计算题、应用题、计数概率题等,要做充分的准备,特别是提高各类计算的熟练度。这样不仅能提高常规题目的正确率,还能为应对复杂问题争取更多时间。
错题反思:考前刷题不应只注重题量,而应在刷题的同时多做错题反思。做会一道错题比盲目多做题更加有用。
审题仔细:对于题干文字量较大的题目,一定要多次审题,标出重点,避免遗漏条件或审题出错。
参考英文题目:尽管中国区考试为双语试卷,还是尽量参照英文题目,避免因翻译错误导致理解偏差。
保持良好状态:考试前应注重休息和饮食安排,尽量将身体和精神状态调整到最佳。
(返回顶部)
六、AMC8竞赛难度分析
AMC8竞赛的难度相对较大,这体现在多个方面:
1. 题目设计
AMC8的题目通常设计得既有趣又具挑战性,旨在全面考察学生的数学知识和思维能力。题目不仅要求学生具备扎实的数学基础,还需要他们具备良好的数学思维和问题解决能力。例如,题目可能设计成趣味性的问题情境,让学生在解题过程中感到既有挑战又有趣味。
2. 知识点覆盖
AMC8竞赛的内容涵盖了多个数学领域,包括数与代数、几何、数论、组合数学以及逻辑推理等。知识点广泛且深入,要求学生全面掌握这些领域的知识,并能够灵活运用它们解决实际问题。例如,学生可能需要在同一道题目中运用代数和几何的知识进行综合解答。
3. 题目难度
AMC8的题目难度通常较高,需要学生具备一定的数学素养和思维能力才能解答。一些题目可能需要学生运用多种数学知识和方法进行推理和计算,才能得出正确答案。例如,某些题目可能涉及复杂的数论或组合数学问题,需要学生具备较强的推理和计算能力。
4. 时间限制
AMC8竞赛的时间限制为40分钟,对于部分学生来说可能比较紧张。学生需要在有限的时间内快速准确地解答25道题目,这对他们的思维速度和解题能力提出了更高的要求。时间管理不当
可能导致部分题目无法完成,从而影响整体成绩。
(返回顶部)
AMC8证书

1、Honor Roll of Distinction AMC8优异证书
——在AMC8竞赛中成绩达到全球前1%。

2、 Honor Roll AMC8优胜证书
——在AMC8竞赛中成绩达到全球前5%。

3、Perfect Score AMC8满分奖
——在AMC8竞赛中成绩达到满分25分。

4、Certificate of Achievement AMC8低年级证书
——六年级及其以下考试参加AMC8且分数在15分及以上。

5、AMC8 参赛证书 Participation
——参赛即可获得。
(返回顶部)
